Integrated logistics models, particularly primary distribution, warehousing and secondary distribution modules, must be built upon a recognition of the unusual characteristics of secondary distribution cost functions, namely, the presence of discontinuous and discrete cost functions. Interesting aspects of the interface between marketing and distribution functions will be addressed. It will be shown that a crucial analysis can be developed by treating fleet capacity, and time utilisation measures of the secondary distribution fleet, as the indicators of change in the direction of solutions being proposed for evaluation. A model is offered to facilitate this analysis.
Introduction
There have been many attempts over recent years to produce simulation models of logistics systems encompassing all steps in the logistics process, from raw material input, to manufacturing through to final customer delivery of finished or semi-finished product. However, any integrated modelling concept has to start somewhere before building its overall design, and it is argued in this article that the tail-end of the logistics process, i.e. customer delivery by vehicle fleets, offers a surprisingly relevant launching point for such model design.
A significant factor in secondary distribution is the presence of discontinuous and discrete cost functions. It can cost anything from zero to several tens of thousands of pounds to effect a marginal customer delivery, depending on how this marginal delivery affects fleet deployment. This discontinuity, even unpredictability, in the secondary distribution cost function is encountered even at the strategic modelling level as well, of course, as at the daily operational level. Essentially, it results from the indivisibility of a vehicle's capacity and shift working time when matched as a resource against the usually more continuous volume and time product demand of the customers. It's important to recognise that these cost discontinuities make a nonsense of standard accounting concepts of average cost, which usually has a more straightforward relationship to a marginal cost function derived from overhead cost amortised over increasing throughput.
In addition, interesting aspects of the interface between marketing and distribution functions will be addressed. It can be shown that a crucial analysis can be developed by treating fleet capacity, and time utilisation measures of the secondary distribution fleet, as the indicators of change in the direction of solutions being proposed for evaluation. For those familiar with operational research techniques, vehicle fleet capacity and time utilisation measures become the 'shadow prices' which determine the direction of change in other marketing and distribution variables in subsequent iterations of the model.
In developing this approach, it is recognised that secondary distribution is, in fact, a very complex problem. One soon realises that, given a relatively simple problem of delivering to 100 locations from a depot, the number of solutions which can be generated by permutations is immense. One could use anything from one vehicle to 100 vehicles! Capacity and time requirements and estrictions then complicate the model, and this increases its complexity.
The fact that such a large number of potential solutions can be calculated is a two-edged sword. To start with, if many solutions are available as they are, then it is never too difficult to find a feasible solution. Secondary distribution management has survived on this blessing for many decades! Equally though, the same truth means that discovery of an optimal solution becomes rather like finding the needle in the haystack. Not only is this search fundamentally important for operational cost efficiency, but it also has to be a component of policy simulation and strategic planning in physical distribution. It is fundamental to economic theory that, when strategic options are being evaluated, each strategic option must be in itself technically efficient or, in economic jargon, each trategic option must be calculated at a local cost optimum, if the strategic planning process is to achieve global optimisation.
Apart from the vehicle capacity and shift time rigidities which introduce their discrete or even capricious marginal cost functions into secondary distribution, there is a further problem arising from the rigidity of the ability to adjust fleet deployment as the resource matched to what is usually an extremely variable and fluctuating demand for product delivery. Thus, customers can and will vary volume and location, frequency and stability of their demand regularly. Dynamic adjustment of the vehicle fleet resource to match such swings will be difficult without operational deployment of efficient computer models, and this becomes a main source and target for cost efficiency in secondary distribution. Once again, the degree to which such efficiency is achieved will affect the abstract average unit costs so central to accounting models of physical distribution. Physical distribution needs, in the first place, to be modelled in physical terms before cost parameters can be attached to the resulting optimal physical deployment of warehouses and vehicles.
In the interaction between marketing and physical distribution functions of a company, it is the marketing function which has long been regarded as the appropriate driving force which should determine the parameters within which physical distribution should operate effectively. This order of priority has, of course, been reflected in the absence of a physical distribution director on corporate boards, a trend which has taken considerable time and growth in awareness to reverse. It soon becomes apparent that treating marketing and physical distribution as a one-way relationship, i.e. one where the marketing decisions unilaterally determine physical distribution decisions produces a corporate strategy which is sales maximising - a position which the economic theory of the firm confirms is not equal to the profit maximising position.
So, for example, at an operational level the salesman will always wish to accept a marginal order, even if the marginal cost in physical distribution terms of effecting its delivery exceeds the gross manufacturing margin for that customer order. It's essential, therefore, to re-integrate marketing and physical distribution functions and to handle them as a simultaneous equation, rather than with a one-way logic. So, although most product companies recognise that physical distribution has been the Cinderella function for too long, and have introduced a significantly more professional input to its management, nevertheless, the recognition that physical distribution should constrain as well as enable marketing in order to achieve a corporate optimum position is not yet widespread.
A fundamental measure of the market profile passed from the marketing function to the physical distribution function, and the measure which allows us to analyse the interaction very effectively is the measure of market concentration. Market concentration can be usefully defined in three dimensions namely those of volume, geographic space or location, and time.
Taking the volume dimension of concentration, it's immediately obvious that a market profile where customer demand is characterised by relatively few customer orders, each of high volume, will produce a much lower unit distribution cost than a market of low volume concentration characterised by a multitude of small volume orders. Equally, a set of customers whose orders are to locations which are very bunched and concentrated geographically, will produce a lower unit distribution cost than a set of customers whose sites are geographically dispersed. Finally, in terms of the time dimension, a given throughput to a customer leads to a lower unit distribution cost if it is concentrated in low frequency bulk orders, i.e. has a concentrated profile in time, rather than if very high frequency orders are imposed, as is the case in many competitive supply markets currently. Unfortunately, the significant increase in unit distribution costs arising from such 'just-in-time' inventory policies, on the part of industrial products customers, is rarely overtly recognised and built into the equations and calculations which affect decisions, implying that unexpected effects will eventually come to bear within the supply side of the industry.
A Diagnostics Measure of Vehicle Fleet Deployment
The following diagram shows a simple comparison of the utilisation of fleet capacity and fleet time for a secondary distribution operation [Figure 1].
It's clear that the target would be for some notional 100% utilisation of both of these dimensions of a fleet's resource, since it is fundamental that high utilisation of units of a resource must imply that the most efficient, normally of course the minimum, number of units has been deployed and, therefore, the cost efficiency is shown in the diagram as the pecked line connecting 100% utilisation of both fleet capacity and shift time.
Target = Maximum Cost Efficiency
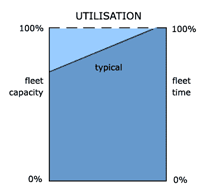 The 'typical' line is then drawn as shown mainly because competitive and procedural pressures have tended to result in a low concentration of the market profile which the physical distribution function has to serve. Therefore, the typical requirement is more likely to be characterised by low volume orders delivered fairly frequently to dispersed geographic sites, than it is by high volume orders delivered as single drop loads at minimum replenishment frequency to concentrated sites. A benefit usually enjoyed by homogeneous liquid and solid aggregate distribution operations, such as petrol and cement.
The 'typical' line is then drawn as shown mainly because competitive and procedural pressures have tended to result in a low concentration of the market profile which the physical distribution function has to serve. Therefore, the typical requirement is more likely to be characterised by low volume orders delivered fairly frequently to dispersed geographic sites, than it is by high volume orders delivered as single drop loads at minimum replenishment frequency to concentrated sites. A benefit usually enjoyed by homogeneous liquid and solid aggregate distribution operations, such as petrol and cement.
The result of this typical low concentration market profile is that when scheduling a vehicle fleet to serve the ultimate order pattern, schedulers find that vehicles run out of shift time well before they run out of capacity. A snapshot of the physical distribution operations of many companies in different industries confirms this typical profile.
Firstly, we can note that the structural market concentration variables are the ones which govern this balance of utilisation of the capacity and time dimension utilisation of the vehicle fleet. This, therefore, makes the vehicle capacity/time utilisation ratio a very simple, but equally powerful, connection and linkage between marketing and physical distribution when these two functions are analysed simultaneously, rather than separately with a subsequent one-way link.
Secondly, it can be seen that the inefficiency in vehicle fleet utilisation expressed by the deviation of the typical line in the diagram from the pecked target maximum cost efficiency line, cannot be addressed unless the marketing/physical distribution interface is re-optimised. Basically, in the picture given above, all the vehicles currently used in the fleet are needed to provide the required aggregate shift time to simply physically get to the deliveries which are dispersed in space and time. It would require an adjustment in the profile of the market structure, i.e. towards fewer orders of higher volume and/or lower frequency in order to permit a deployment of the fleet which reduced the fleet time utilisation measure, hence bringing the 'typical' line more into parallel with the base of the diagram. Once this had been achieved, vehicles could then be made redundant from the fleet in order to raise the line towards the target of maximum cost efficiency.
At the very least, such a model then gives strategic information from the physical distribution function, back to the marketing function of the company, on the exact cost implications of its chosen marketing strategy and the resultant customer order profiles. In general, then, market concentration and physical distribution unit cost are inversely related.
Elements for an Integrated Model
We can now set out how this simple diagnostic of the balance between fleet time and capacity utilisation can be used to drive a model which is searching through more global distribution and marketing adjustments. Variables which are important in most physical distribution decisions include: actual productivity at delivery site (ie call time), the mix of vehicle sizes deployed in the fleet, the number of depots to cover a given territory, the trips per day ratio. Marketing variables which must be included in the analysis are: Product range, Order volume, Delivery frequency, Extent of the set of customers, Minimum order value regime, Geographical coverage developed and Product pricing.
The table below shows how adjustments in these central distribution and marketing variables can be related into a global optimisation by searching through solutions, and then measuring each solution in terms of the simple diagnostic developed above of the balance of utilisation of fleet capacity and time.
| Adjustments in Distribution & Marketing in Response to Fleet Efficiency Diagnostics |
||
| TIME USE> CAPACITY USE |
TIME USE> CAPACITY USE |
|
| Distribution adjustments |
Increase productivity | |
| Smaller vehicles | Larger vehicles | |
| More depots (quasi) | Fewer Depots | |
| More multi-day trips | Fewer multi-day trips | |
| Pre-loading/demounts | ||
| Marketing adjustments |
Extend product range | Reduce products |
| Increase volume per call | ||
| Decrease frequency | Increase frequency | |
| Reduce customer set | Increase customers | |
| Raise minimum order value | Reduce minimum | |
| Reduce geographical coverage | Broaden geographical coverage | |
| Price down | Price up | |
Working through these, one can see that when a fleet runs out of its shift time before it runs out of its capacity, then enhanced productivity at actual deliveries will effect a structural release of resources. Therefore, equipping vehicles with self-stack unloading devices may be an appropriate solution, or else calling at delivery sites at a pre-specified time may be found to reduce call time compared with arriving at random time.
The snapshot observation of time utilisation greater than capacity utilisation would also suggest smaller, rather than larger, vehicles in the fleet mix. It may also suggest that a simulation is run with relatively more depots specified. This is because fewer depots will obviously impose 'stem times' on all secondary delivery trips, and could thus be the pivotal issue responsible for the secondary distribution fleet hitting shift time constraints well before capacity is used. Increased number of depots need not be in terms of stocked depots but could, of course, be the use of more stockless satellites.
A similar consideration suggests that more multiple day trips in a secondary distribution operation would be useful, in that once a stem driving time has been incurred, then it becomes more efficient to keep a vehicle in an area for a further day(s) in order to use its capacity to cover more orders in that area. Obviously, ensuring that loading time is outside, rather than within a vehicle's shift by the use of demountable body technology, will also be an effective relief to the structural condition where time utilisation constraints are met before capacity utilisation.
This simple fleet diagnostic basically represents an under-utilised network, so that if the marketing function can extend the product range by distributing complementary products to the same customer delivery sites, then the extension product range will have been distributed effectively at zero marginal cost, certainly in sheer secondary physical distribution terms and, therefore, contributes significantly to corporate profitability.
Marketing policy should be directed to increase the volume per call, and decreased delivery frequencies would clearly be effective to this end, even if they are applied selectively to customer accounts. Indeed, recent attention has focused much emphasis on the concept of customer profitability, and the more exact marginal rather than average cost of physical distribution, once allocated to customer accounts, may quickly identify certain customers in total account terms as being very unprofitable to service. This will result more often from financial costing based upon physical modelling, than it will from abstract average costing of physical distribution to customer accounts; and this simple fleet efficiency diagnostic may, once again, have a strategic effect in suggesting a reduction of the customer set.
The raising of minimum order values can also be simulated, with the additional advantage that optimum break points in quantity discount pricing will themselves be identified by the modelling work. Geographical coverage should also be reduced in subsequent iterations of the model if this is a variable factor. Finally, simple price reductions may well generate increased volume throughput and, therefore, higher volume per delivery. The price reduction with its inherent reduction in gross manufacturing margin may well be found to be more than compensated for by the reduced physical distribution cost achieved by the enhanced efficiency in fleet deployment.
Each of these adjustments has its corollary when the snapshot picture of fleet deployment shows that the capacity constraint is being met well in advance of the shift time utilisation approaching 100%. Thus, this would indicate that subsequent iterations of the simulation model should try larger vehicles within the fleet mix, fewer depots with derived greater trip stem times, and multiple trip working within a daily vehicle shift. In fact, in operations characterised by single drop working, petrol deliveries being a good example, efficiency is usually identifiable as the result of more optimum management of multiple tripping of vehicles within their daily shift.
In the same way, the fleet efficiency diagnostic suggests reduction of the product range, increased delivery frequencies which will undoubtedly have a competitive benefit in the market-place, as well as being freely available from a distribution operation which has run out of vehicle capacity rather than time. The customer set could be happily increased, reduced minimum order values accepted, and the geographical coverage extended. Finally, the surprising result is that a price increase could be contemplated as a way of choking off any excess demand which is distorting the secondary vehicle fleet deployment, and causing structural inefficiencies in physical distribution with higher unit costs.
Conclusion
These concepts have formed the basis for repeated and successful optimising simulation work covering the marketing/physical distribution interface in a number of companies across several industry sectors, both in the UK and internationally. There is continued scope for the application of this approach within U.K. markets, but an even greater opportunity in applying the methodology to the pan-European market.
It is the contention of this article that efficient simulation tools must include physical optimisation modules, specifically accurate and optimal computer vehicle scheduling models of the secondary vehicle fleet. This approach, which could be characterised as 'bottom up' rather than 'top down' is argued to be necessarily superior, both intellectually and practically, to the abstract average cost models which ave been developed and often applied to integrated logistics modelling work. As has been demonstrated, such models can always find another feasible solution, but since they include a fundamental error in their specification by ignoring the discrete if not capricious nature of the secondary distribution cost function, they cannot be demonstrated to have worked uniquely towards optimality.
©Geoff Crocker
| Copyright © Technology Market Strategies 2003 | |
| tel UK | +44 (0)7770 585 031 |
| tel Moscow | (+7 095) 103 7800 |
| geoff.crocker@tms.eu.com | |